TEOREMA DE PITÁGORAS
PITAGORAS:
Pitágoras de Samos 569 a. C. – 475 a. C. fue un filosofo y matemático griego considerado el primer matemático puro. Contribuyó en el avance de la matemática elenica , la geometría y la aritmética, derivadas particularmente de las relaciones numéricas, y aplicadas por ejemplo a la teoría de pesos y medidas, a la teoría de la música o a la astronomía. Es el fundador de la Hermandad Pitagórica, una sociedad que, si bien era de naturaleza predominantemente religiosa, se interesaba también en medicina, cosmología, filosofía, ética y política, entre otras disciplinas. El pitagorismo formuló principios que influyeron tanto en Platon como en Aristoteles y, de manera más general, en el posterior desarrollo de la matemática y en la filosofía racional en Occidente.
Piramide de Kefren
primera construcción aplicando el teorema de pitagoras; construida en el siglo xxvi a.c, por los egipcios.
En un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados (llamamos "triángulo rectángulo" a un triángulo con un ángulo recto)
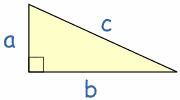 |
a2 + b2 = c2
|
¿QUIÉN DESCUBRIÓ EL TEOREMA DE PITÁGORAS?
La respuesta parece sencilla: Pitágoras claro. Al menos él fue el que lo elaboró y el que realizó la demostración matemática. Sin embargo, la relación entre los lados de un triángulo rectángulo parece que ya se conocía desde varios siglos antes. En Nueva York se conservan unas tablillas babilónicas de repartos de tierras, grabadas 2500 años antes de pitágoras,que según los científicos que las han estudiado demuestran que en aquella época ya se utilizaba el famoso teorema de Pitágoras,aunque no quedase expresamente formulado y demostrado hasta que Pitágoras lo hizo.
Pero algo nos hace dudar:Hay cierta controversia acerca de si Pitágoras fue el primero en demostrar el teorema, pues se sabe de la existencia una demostración publicada en la obra matemática Chou Pei, de origen Chino, pudiendo ser ésta anterior a Pitágoras, aunque se cree que no llegó a conocer esta obra.
Demostración
El Teorema de Pitágoras es de los que cuentan con un mayor número de demostraciones diferentes, utilizando métodos muy diversos. Las demostraciones están divididas en cuatro grandes grupos: las algebraicas, donde se relacionan los lados y segmentos del triángulo; geométricas, en las que se realizan comparaciones de
áreas; dinámicas a través de las propiedades de fuerza, masa; y las cuaterniónicas, mediante el uso de vectores.
Demostración de Bhaskara:
Bhaskara II, matemático y astrónomo hindú del siglo XII, da la siguiente demostración del teorema de Pitágoras. Con cuatro triángulos rectángulos de lados a, b y c se construye el cuadrado de lado c –izquierda-, en cuyo centro se forma otro cuadrado de lado (a-b). Redistribuyendo los cuatro triángulos y el cuadrado de lado (a-b), construimos la figura de la derecha, cuya superficie resulta ser la suma de la de dos cuadrados: uno de lado a –azul- y otro de lado b -naranja-. Se ha demostrado gráficamente que c2=a2+b2 Algebraicamente: el área del cuadrado de lado c es la correspondiente a los cuatro triángulos, más el área del cuadrado central de lado (a-b), es decir: c2=4 * ab/2+ (a-b) 2expresión que desarrollada y simplificada da el resultado c2=a2+b2, y el teorema queda demostrado.
Polígono ADEFGB: la línea DG lo divide en dos mitades idénticas, ADGB y DEFG.El
Leonardo da Vinci: Partiendo del triángulo rectángulo ABC con los cuadrados de catetos e hipotenusa, Leonardo añade los triángulos ECF y HIJ, iguales al dado, resultando dos polígonos, cuyas superficies va a demostrar que son equivalentes:
Un polígono ACBHIJ: la línea CI determina CBHI y CIJA.
- Se aprecia de inmediato que tienen tres lados iguales: AD=AC, AB=AJ, BG=BC=IJ
- Asimismo es inmediata la igualdad entre los ángulos de los siguientes vértices:
- A de ADGB y A de CIJA
- B de ADGB y J de CIJA.
Demostración
Sea el triángulo rectángulo de catetos a y b e hipotenusa c. Se trata de demostrar que el área del cuadrado de lado c es igual a la suma de las áreas de los cuadrados de lado a y lado b. Es decir: a2 + b2 = c2 Si añadimos tres triángulos iguales al original dentro del cuadrado de lado c formando la figura mostrada en la imagen, obtenemos un cuadrado de menor tamaño. Se puede observar que el cuadrado resultante tiene efectivamente un lado de b - a. Luego, el área de este cuadrado menor puede expresarse de la siguiente manera: (a-b)2 = a2 - 2ab + b2 Ya que (b-a)2 = (a-b)2 Es evidente que el área del cuadrado de lado c es la suma del área de los cuatro triángulos de altura a y base b que están dentro de él más el área del cuadrado menor: c2 = 4 *( a * b/2) + a2 - 2ab + b2= a2 + b2 y así ha quedando demostrado el teorema.
Comparando los polígonos destacados en gris, ADGB y CIJA:
Se concluye que ADGB y CIJA son iguales. De modo análogo se comprueba la igualdad entre ADGB y CBHI. Además, un giro de centro A, y sentido positivo, transforma CIJA en ADGB. Mientras que un giro de centro B, y sentido negativo, transforma CBHI en ADGB. Todo ello permite establecer que los polígonos ADEFGB y ACBHIJ tienen áreas equivalentes. Si a cada uno se le quita sus dos triángulos –iguales- las superficies que restan forzosamente serán iguales. Y esas superficies no son sino los dos cuadrados de los catetos en el polígono ADEFGB, por una parte, y el cuadrado de la hipotenusa en el polígono ACBHIJ, por la otra. El teorema de Pitágoras queda demostrado.







